Welcome back to Do Science! In this post, we're going to discuss some more things about sets. If you missed the first part, click on the tag and it will take you to the earlier post. Without further ado,
Operations with Sets: (Nothing to do with surgery)
1) Union of Sets: The first thing that comes to my mind when I hear union of sets is a marriage of sorts between two sets. The symbol for 'union' looks like that too, we symbolize this operation like this: X∪Y, and if you look at this it kind of looks like X and Y (which represent sets) are holding hands. Basically, take the elements of both the sets that you are supposed to unionize (unionize? is it a word?) and make it into one big set.
X={1, 2, 3}
Y={3, 4, 5}
X was a lonely set searching for love, and one day he logged onto an online dating site, where he posted his details like the type and number of his elements. He met Y there because they had the element '3' in common, and they decided to get married.
Soon, they were blessed with a bouncing healthy baby set, Z, and Z could be defined as:
Z={1,2,3,4,5}.
Z is THE UNION of the two sets X and Y.
Of course, this also works with sets of different cardinalities (Gosh, calm down, it's just a new word. Cardinality just means the number of elements there are in a set.), and between sets which have no elements in common at all.
If you like circles (I'm more of a triangles person myself, personally), then we can represent this operation with a Venn diagram.
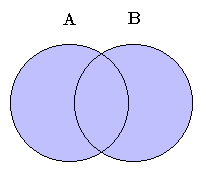
2) Intersection of Sets: This is another easily visualized concept. Imagine two roads. The point where the two roads cross each other is known as the intersection. Both roads may cover miles and miles of space that are completely unrelated, but the intersection is only concerned with the area they both cover, or the common area.
An intersection is represented like this: A∩B
Things always make more sense to me when I see them in numbers, so, again, let's consider the same set X and Y. We've already seen that these sets have the number '3' in common, therefore, X∩Y={3}
The Venn diagram for this is:
All good so far? It's not time to rejoice yet, there's lots more. Now, we will move on to the fancier terms with which you can easily impress simple-minded people by randomly injecting them into unrelated sentences.
3) Complement of a Set:
First, let's discuss the things that this is not.
Operations with Sets: (Nothing to do with surgery)
1) Union of Sets: The first thing that comes to my mind when I hear union of sets is a marriage of sorts between two sets. The symbol for 'union' looks like that too, we symbolize this operation like this: X∪Y, and if you look at this it kind of looks like X and Y (which represent sets) are holding hands. Basically, take the elements of both the sets that you are supposed to unionize (unionize? is it a word?) and make it into one big set.
X={1, 2, 3}
Y={3, 4, 5}
X was a lonely set searching for love, and one day he logged onto an online dating site, where he posted his details like the type and number of his elements. He met Y there because they had the element '3' in common, and they decided to get married.
Soon, they were blessed with a bouncing healthy baby set, Z, and Z could be defined as:
Z={1,2,3,4,5}.
Z is THE UNION of the two sets X and Y.
Of course, this also works with sets of different cardinalities (Gosh, calm down, it's just a new word. Cardinality just means the number of elements there are in a set.), and between sets which have no elements in common at all.
If you like circles (I'm more of a triangles person myself, personally), then we can represent this operation with a Venn diagram.
2) Intersection of Sets: This is another easily visualized concept. Imagine two roads. The point where the two roads cross each other is known as the intersection. Both roads may cover miles and miles of space that are completely unrelated, but the intersection is only concerned with the area they both cover, or the common area.
An intersection is represented like this: A∩B
Things always make more sense to me when I see them in numbers, so, again, let's consider the same set X and Y. We've already seen that these sets have the number '3' in common, therefore, X∩Y={3}
The Venn diagram for this is:
3) Complement of a Set:
First, let's discuss the things that this is not.
Complement of a set is not "your hair looks nice today." We're thinking more along the lines of Yin and Yang. That's right, sets are also involved in ancient Chinese philosophy.
One is what the other is not and they exist with each other in a beautiful balance. In less poetical language that is probably more accurate also, complement of a set is basically a set containing all the elements outside the set of which we are finding the complement.
Again, this is not as complicated as it sounds. Consider the problem of the numbers from one to five. We have a set A, which contains only the element '3'.
A={3}
The complement of this set, which can be represented as A', contains all the elements BESIDES the elements of A in the universal set.
Therefore, A'={1, 2, 4, 5}
That's all for today, folks! I was going to make this more detailed but illustrating that joke really tired me out. Hope this helps any of you who need this information for passing tests and things. Also, if they ask you to define 'complement of a set' in your exam, PLEASE do not write any of the things I said above. Peace and love! Have a good Tuesday!
No comments:
Post a Comment