Science for Ignoramuses: Set Theory II

    Welcome back to Do Science! In this post, we're going to discuss some more things about sets. If you missed the first part, click on the tag and it will take you to the earlier post. Without further ado,

Operations with Sets: (Nothing to do with surgery)

1) Union of Sets: The first thing that comes to my mind when I hear union of sets is a marriage of sorts between two sets. The symbol for 'union' looks like that too, we symbolize this operation like this:  X∪Y, and if you look at this it kind of looks like X and Y (which represent sets) are holding hands. Basically, take the elements of both the sets that you are supposed to unionize (unionize? is it a word?) and make it into one big set.
X={1, 2, 3}
Y={3, 4, 5}
X was a lonely set searching for love, and one day he logged onto an online dating site, where he posted his details like the type and number of his elements. He met Y there because they had the element '3' in common, and they decided to get married.
Soon, they were blessed with a bouncing healthy baby set, Z, and Z could be defined as:
Z={1,2,3,4,5}.
Z is THE UNION of the two sets X and Y.

Of course, this also works with sets of different cardinalities (Gosh, calm down, it's just a new word. Cardinality just means the number of elements there are in a set.), and between sets which have no elements in common at all.

If you like circles (I'm more of a triangles person myself, personally), then we can represent this operation with a Venn diagram.                                  
                                          











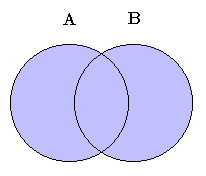
2) Intersection of Sets: This is another easily visualized concept. Imagine two roads. The point where the two roads cross each other is known as the intersection. Both roads may cover miles and miles of space that are completely unrelated, but the intersection is only concerned with the area they both cover, or the common area.
An intersection is represented like this: A∩B
Things always make more sense to me when I see them in numbers, so, again, let's consider the same set X and Y. We've already seen that these sets have the number '3' in common, therefore,    X∩Y={3}
 The Venn diagram for this is:

All good so far? It's not time to rejoice yet, there's lots more. Now, we will move on to the fancier terms with which you can easily impress simple-minded people by randomly injecting them into unrelated sentences.

3) Complement of a Set: 
           First, let's discuss the things that this is not.

Complement of a set is not "your hair looks nice today." We're thinking more along the lines of Yin and Yang. That's right, sets are also involved in ancient Chinese philosophy. 

One is what the other is not and they exist with each other in a beautiful balance. In less poetical language that is probably more accurate also, complement of a set is basically a set containing all the elements outside the set of which we are finding the complement.

            Again, this is not as complicated as it sounds. Consider the problem of the numbers from one to five. We have a set A, which contains only the element '3'.

A={3}

The complement of this set, which can be represented as A', contains all the elements BESIDES the elements of A in the universal set.

Therefore, A'={1, 2, 4, 5}

That's all for today, folks! I was going to make this more detailed but illustrating that joke really tired me out. Hope this helps any of you who need this information for passing tests and things. Also, if they ask you to define 'complement of a set' in your exam, PLEASE do not write any of the things I said above. Peace and love! Have a good Tuesday!

Science For [Insert Politically Correct Term For 'Dummies']: Set Theory I

      Good morning, ladies and gentlemen in the Asian Pacific region, and good whatever-time-it-is-in-your-heathen-countries to the rest of the world. Today, we are going to Do Science.
 
   Science is a very valuable and useful thing that humans use everyday, mostly for torturing poor students with fragments of the truth that are impossible to understand but also for wonderful and noble pursuits like figuring out whether buying a lottery ticket is a good idea (of course it is!), and whether or not you should grasp a hot plate directly with wet hands (don't do it).

    See how much we've learned already? Science, people! It's important! Therefore, in the interests of making the world a better place, today I am going to explain to you the concept of sets, which is a very interesting (no, really, it is! Please don't stop reading) theory that kind of explains everything else in Mathematics. So, once you've got this, you're pretty much sorted.

    The first gentleman to think about sets was not Georg Cantor (I know how to spell 'George', m'kay, his parents couldn't), but he was the first man to show why they were important and formally propose set theory. He was a German with a fancy beard and he said that 'a set is any collection into a whole of definite and distinct objects of our intuition or thought.'

    There were some problems with Cantor's set theory though (notably the Russell paradox, which we shall discuss later), and in recent years it has been called the 'naive set theory' (ouch!). The modern definiton of sets is 'a set is a collection of objects which are distinct and distinguishable'.

    Now, forget about the big words and the fancy numbers and all of that. Let's just think about common, everyday things, which is really what math is about in the first place. We use sets everyday! For example, if someone asks you who your best friends are, you might say, "My best friends are Adrian, Rose and Geetanjali.'

    That, ladies and gentlemen, is a set. Does it fulfill all the conditions of a set? Let's check: first, it's a collection (of people sad enough to be friends with you), second the objects are distinct or non-repeated (unless Rose and Geetanjali are the other personalities of Adrian who is a schizophrenic, in which case some people might argue that this is not a set, and also, you probably need some more friends), and finally, the objects are distinguishable, in other words, we are able to decide whether they belong to the set or not. Consider Natalie. Is she one of your best friends? Whether the answer is, "No, and the bitch had better watch her back', or 'yes, we are totes BFFz', it proves that you are able to decide whether the object, Natalie, belongs to your set of best friends or not. Therefore, this meets all the conditions of being a set.

   Simple, right? So what do all these terms like interjection, bijection, inverted and onto-onto mean? Patience, friends, I shall tell you.

First, let's discuss the different types of sets.

1) The Null Set: If you asked an unpopular person who their friends are, they would have to say, while weeping copiously, that they have no friends. We can represent this like this, A={}, where 'A' is the name we give the set of Sad Loser's friends, and the '{}' brackets contain the elements of this set. This set is empty, therefore we call it a null set.

2) The Finite Set: My textbook very helpfully describes this as a set that has a finite number of elements. Thanks, textbook. I would never have guessed that on my own. Finite basically means a number you can count or imagine, like the number of days left before my CET exam which I really should be preparing for.

3) The Infinite Set: My textbook again brilliantly describes this as a set which is not a finite set. *slow sarcastic applause*. In other words, this is a set of elements which are countless in number. Like a set of the number of stars in the sky, or the stress acne on my face because of these freaking exams.

4) The Universal Set: The universal set is basically the set of EVERYTHING. Of course, the definition of everything varies depending on the problem you're considering. If you're considering the problem of Indian politicians, say, we can define the universal set of this problem as the set of all the politicians in India, and this is a large set, but not an infinite one (thank goodness). However, if we're considering the problem of natural numbers (you know what natural numbers are. One, two, three, four.. It's not rocket science), this is an infinite set for obvious reasons.

5) The Subset: Nothing to do with sandwiches, unfortunately. Using the example given above, we can define a subset as a set, the elements of which are all elements of another set. Confused? A subset of Indian politicians, say B, can be defined as B={Narendra Modi, Rahul Gandhi, Arvind Kejriwal}. Each of the elements of this set B, is an element of the set 'Indian Politicians', therefore B is a subset of the universal set of Indian politicians. Kapish?

And those are some of the basics of set theory! There, that wasn't so hard, was it? We'll move on to operations in the next class, until then, have a good Thursday!